Soal Dinamika Benda Tegar dan Pembahasannya

Soal Dinamika Benda Tegar dan Pembahasannya - Dalam fisika, dinamika benda tegar adalah studi tentang gerak benda yang tidak mengalami deformasi. Misalnya, untuk menentukan massa beban agar sistem batang XY bermassa 5 kg tetap seimbang, kita dapat menggunakan prinsip kesetimbangan torsi. Ini adalah salah satu dari banyak soal yang menguji pemahaman tentang keseimbangan rotasi dan translasi. Artikel ini menguraikan berbagai soal dan pembahasan terkait dinamika benda tegar, membantu Anda memahami konsep fundamental dan aplikasinya dalam berbagai situasi fisika.

Soal dinamika benda tegar no 1

Perhatikan gambar berikut!

P adalah titik berat batang xy yang bermassa 5 kg. Jika sistem dalam keadaan seimbang, massa beban B adalah ….

A. 5 kg

B. 4 kg

C. 3 kg

D. 2 kg

E. 1 kg

Pembahasan dinamika benda tegar :

Perhatikan gambar berikut:

Untuk mengetahui massa beban B maka menggunakan jumlah torsi terhadap titik x harus sama dengan nol.

$$\begin{align*} \Sigma \tau &= 0 \\ w\cdot 2 - F\cdot 5 &= 0 \\ 50\cdot 2 - F\cdot 5 &= 0 \\ 100 &= F\cdot 5\\ F &= 20 \quad \textrm{N}\\ \end{align*}$$

Nilai F sama dengan berat B, maka massa B = 2 kg.

Jawaban : D

Soal No. 2

Sebuah tangga homogen dengan berat 300 N bersandar pada sebuah dinding licin. Kaki tangga terletak pada lantai kasar . Tangga akan tergelincir jika seseorang yang beratnya 450 N menaiki tangga sampai jarak 2 m dari kaki tangga . Koefisien gesek antara tangga dan lantai tersebut adalah …..

A. 0,27

B. 0,30

C. 0,33

D. 0,36

E. 0,39

Pembahasan :

Perhatikan gaya-gaya yang bekerja berikut:

Dari gambar dapat diketahui bahwa :

$$\begin{align*} \sin \theta &= \frac{4}{5} \\ \cos \theta &= \frac{3}{5} \\ \tan \theta &= \frac{4}{3} \end{align*}$$

Agar orang yang menaiki tangga tidak tergelincir maka sistem harus setimbang rotasi maupun translasi, misalkan ditentukan poros di A :

Kesetimbangan rotasi terhadap titik A:

$$\begin{align*} \Sigma \tau _A &= 0 \\ N_B \sin \theta \cdot 5 - w_{papan}\cdot \cos \theta \cdot 2,5 - w_{orang} \cdot \cos \theta \cdot 2 &= 0 \\ N_B \cdot \frac{4}{5} \cdot 5 - 300\cdot \frac{3}{5} \cdot 2,5 - 450 \cdot \frac{3}{5}\cdot 2 &= 0 \\ 4N_B - 450 - 540 &= 0 \\ 4N_B &= 990\\ N_B &= 247,5 \quad \textrm{N}\\ \end{align*}$$

Kesetimbangan translasi :

Kesetimbangan terhadap sumbu y :

$$\begin{align*} \Sigma F_y &= 0 \\ N_A - w_{papan} - w_{orang} &= 0 \\ N_A - 300 - 450 &= 0 \\ N_A &= 750 \quad \textrm{N} \end{align*}$$

Kesetimbangan terhadap sumbu x :

$$\begin{align*} \Sigma F_x &= 0 \\ N_B - f_{gesek} &= 0 \\ N_B &= f_{gesek} \\ N_B &= \mu \cdot N_A \\ \mu &=\frac{N_B}{N_A} \\ &=\frac{247,5}{750} \\ &= 0,33 \end{align*}$$

Jadi koefisien gesek antara tangga dan lantai tersebut adalah : μ = 0,33

Jawaban soal nomor 2 tentang dinamika benda tegar adalah : C

Soal No. 3 : Katrol silinder pejal.

Perhatikan gambar berikut.

Besar tegangan tali T_A dan T_B adalah ….

A. 35 N dan 30 N

B. 30 N dan 35 N

C. 30 N dan 25 N

D. 25 N dan 30 N

E. 20 N dan 25 N

Pembahasan tentang katrol silinder pejal :

$$\begin{align*} \Sigma \tau &= I\alpha \\ T_B \cdot R - T_A \cdot R &= I\alpha \\ T_B \cdot R - T_A \cdot R &= \frac{1}{2}MR^2 \cdot \frac{a}{R} \\ T_B - T_A &= \frac{1}{2}M a \quad \textrm{................................ (1)} \end{align*}$$

Sistem benda A :

$$\begin{align*} \Sigma F &= m_A a \\ T_A - w_A &= m_A a \\ T_A - 20 &= 2a \\ T_A &= 2a + 20 \quad \textrm{................................ (2)} \end{align*}$$

Sistem benda B :

$$\begin{align*} \Sigma F &=  m_B a \\ T_B - w_B &= 4(-a) \\ T_B - 40 &= -4a \\ T_B &= 40 - 4a \quad \textrm{................................ (3)} \end{align*}$$

Substitusikan persamaan (2) dan (3) ke persamaan (1) sehingga :

$$\begin{align*} T_B - T_A &=  \frac{1}{2}M a \\ 40-4a - (2a+20) &= \frac{1}{2}\cdot 4 a \\  40- 4a - 2a - 20 &= 2 a \\ 20 &= 8 a \\ a &=  2,5 \quad \textrm{m/s}^2 \end{align*}$$

Tegangan Tali A :

$$\begin{align*} T_A &= 2a + 20 \\ &= 2\cdot 2,5 + 20 \\  &= 25  \quad \textrm{N}\end{align*}$$

Tegangan Tali B :

$$\begin{align*} T_B &= 40 - 4a \\ &= 40 - 4\cdot 2,5 \\  &= 30  \quad \textrm{N} \end{align*}$$

Jawaban soal katrol silinder pejal : D

Soal Nomor 4:

Perhatikan gambar berikut.

Gambar tersebut menunjukkan sebuah silider pejal yang menggelinding turun pada sebuah bidang miring. Kecepatan silinder pejal di ujung lintasan adalah ….

A. 8 m/s

B. 6 m/s

C. 4 m/s

D. 2 m/s

E. 1 m/s

Pembahasan soal silinder pejal yang menggelinding turun pada sebuah bidang miring :

Menggunakan Hukum Kesetaraan Energi :

Diketahui momen inersia silinder pejal :   $I=\frac{1}{2}mR^2$

$$\begin{align*} Ek_1 + Ep_1 &= Ek_2 + Ep_2 + Ek_{rot} \\ 0 + mgh &= \frac{1}{2}mv^2 + 0 + \frac{1}{2}I\omega ^2 \\ mgh &= \frac{1}{2}mv^2 +  \frac{1}{2}\cdot \frac{1}{2}mR^2\cdot (\frac{v}{R})^2 \\ gh &= \frac{1}{2}v^2 +  \frac{1}{4}\cdot v^2 \\ 10\cdot 2,7 &= \frac{3}{4}v^2  \\ 27 &= \frac{3}{4}v^2  \\ v^2 &= \frac{4}{3}\cdot 27 \\v^2 &= 36 \\v &=6 \quad \textrm{m/s} \\\end{align*}$$

Jawaban : B

Soal Dinamika Benda Tegar No. 5

Sebuah benda berupa silinder pejal bermassa 8 kg dan berjari-jari 5 cm ditarik dengan gaya F = 180 N seperti gambar berikut.

Apabila terjadi gesekan antara silinder dengan lantai, percepatan linear yang terjadi adalah ….

A. 15 m/s²

B. 5 m/s²

C. 4 m/s²

D. 2,5 m/s²

E. 2 m/s²

Pembahasan :

Perhatikan gaya-gaya yang bekerja :

Gerak Rotasi :

$$\begin{align*} \Sigma \tau &= I\alpha \\ f_g R &= \frac{1}{2}mR^2 \frac{a}{R} \\  f_g &= \frac{1}{2}ma \\  f_g &= \frac{1}{2}\cdot 8\cdot a \\ f_g &= 4a \end{align*}$$

Gerak tanslasi :

$$\begin{align*} \Sigma F &= ma \\ F - f_g &= 4a \\  F -4a &= 8a \\  F &= 12a \\180 &= 12a \\a &= \frac{180}{12} \\ &= 15 \quad \textrm{m/s}^2 \end{align*}$$

Jawaban Soal Dinamika Benda Tegar No. 5 : A

Soal No. 6 :

Batang AB homogen dengan berat 400 N terikat pada tali dengan ujung yang satu berengsel pada ujung yang lain.

Pada batang tersebut digantungkan beban 600 N sehingga setimbang. Panjang AB = 3 m , AD = 1,6 cm dan AC = 1,2 m sehingga besar tegangan talinya adalah …..

A. 1.600 N

B. 2.000 N

C. 2.500 N

E. 2.800 N

D. 3.200 N

Pembahasan :

Menggunakan trigonometri :

$$\begin{align*} CD^2 &=  AC^2 + AD^2 \\ &=   1,2^2 + 1,6^2 \\ &=   4 \\ CD &=  2 \quad \textrm{m}\\\end{align*}$$

Misalkan poros di A , maka :

$$\begin{align*} \Sigma \tau _A &=  0 \\ w_{batang} \cdot 1,5 + w_{beban} \cdot 3 - T \sin \theta \cdot 1,2&=  0 \\ 400 \cdot 1,5 + 600 \cdot 3 - T \cdot {1,6}{2} \cdot 1,2&=  0 \\ 600 + 1.800 - 0,96T &=  0 \\0,96T &=   2.400\\ T &=  2.500 \quad \textrm{N}\\\end{align*}$$

Jawaban : C

Soal No. 7 tentang yoyo :

Perhatikan gambar berikut.

Roda katrol pejal C berputar melepaskan diri dari lilitan tali. Massa roda adalah 300 g. Jika g = 10 m/s², besar tegangan tali T adalah ….

A. 1 N

B. 1,5 N

C. 2 N

D. 3,3 N

E. 4 N

Pembahasan :

Gerak rotasi :

$$\begin{align*} \Sigma \tau  &=  I\alpha \\ TR &=  \frac{1}{2}mR^2 (\frac{a}{R}) \\ T&=  \frac{1}{2}ma \\&=  \frac{1}{2}\cdot 0,3\cdot a \\&=  0,15 a \end{align*}$$

Gerak translasi :

$$\begin{align*} \Sigma F  &= ma \\ T-w&=  0,3(-a) \\ T - 3&=  -0,3a \\ 0,15a -3&= -0,3a \\0,45a &= 3 \\a&=\frac{20}{3} \quad \textrm{m/s}^2\end{align*}$$

Besar tegangan tali :

$$\begin{align*} T&=  0,15 a  \\ &=  0,15\cdot \frac{20}{3} \\ &=  1 \quad \textrm{N}\end{align*}$$

Jawaban : A

Soal  Nomor 8 : SPMB Fisika tahun 2006

Seutas tali dililitkan pada sebuah roda. Tali ditarik sehingga roda berputar. Roda tersebut berdiameter 0,5 m. Dengan momen inersia 10 kg.m2, dab berputar pada porosnya tanpa gesekan. Tegangan tali 40 N dikerjakan pada tepi roda. Jika roda diam saat t = 0, panjang tali yang tak tergulung pada saat t = 3 s adalah ....

A. 2,250 m

B. 1,125 m

C. 0,57 m

D. 0,28 m

E. 0,14 m

Pembahasan :

$$\begin{align*} \Sigma \tau &=  I\alpha  \\ F\cdot R&=   I\alpha \\ 40\cdot 0,25&=   10\alpha \\ 10&=   10\alpha \\ \alpha &=  1 \quad \textrm{rad/s}^2\end{align*}$$

Panjang tali :

$$\begin{align*} s &=  \frac{1}{2}at^2  \\ &=  \frac{1}{2}\alpha \cdot R\cdot t^2  \\ &=  \frac{1}{2}\cdot 1 \cdot 0,25 \cdot 3^2  \\ &=   1,125 \quad \textrm{m}\end{align*}$$

Jawaban : B

Soal  Nomor 9 : SPMB Fisika tahun 2007

Sebuah batang XY yang beratnya 10,0 N bertumpu pada tembok di X. Batang ditahan secara horisontal oleh gaya F yang bekerja di Y dan membentuk sudut 60^o terhadap arah vertikal seperti ditunjukkan oleh gambar. Berapa besar F?

A. 20,0 N

B. 10,0 N

C. 8,66 N

D. 5,00 N

E. 4,33 N

Pembahasan :

Kesetimbangan rotasi dengan poros di X :

$$\begin{align*} \Sigma \tau _x &=  0  \\ w\cdot \frac{1}{2}L - F\cos 60 \cdot L &=   0 \\ 10\cdot \frac{1}{2}L - 0,5F\cdot L &=   0 \\ 5L - 0,5F\cdot L &=   0 \\ 5L&=   0,5F\cdot L \\ 5&=   0,5F \\ F&=\frac{5}{0,5} \\&=  10 \quad \textrm{N}\end{align*}$$

Jawaban : B

Soal Nomor 10 : UM-UGM Fisika Tahun 2007

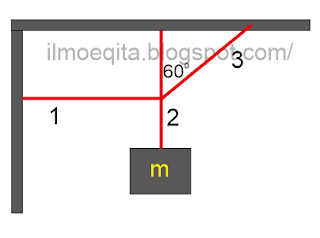
Sebuah balok bermassa m digantung dengan tiga utas tali seperti terlihat dalam gambar dibawah.

Besar tegangan tali (1) adalah ....

A. $\sqrt{3}$ mg

B. $\frac{1}{2}\sqrt{3}$ mg

C. $\frac{1}{2}$ mg

D. $\frac{1}{3}$ mg

E. $\frac{1}{4}$ mg

Pembahasan :

Kesetimbangan sumbu x :

$$\begin{align*} \Sigma F _x &=  0\\ F_{3x} - F_{1x} &=   0 \\ F_{1x} &=   F_{3x} \\ F_{1x} &=   F_3 \sin 60 \\ &=  \frac{1}{2}\sqrt{3} F_3 \quad \textrm{........................... (1)}\end{align*}$$

Kesetimbangan sumbu y :

$$\begin{align*} \Sigma F _y &=  0\\ F_{3y} - F_{2y} &=   0 \\ F_{3y} &=  F_{2y}\\ F_3\cos 60 &=   w \\ \frac{1}{2}F_3&=  mg \\ F_3 &= 2mg \quad \textrm{............................ (2)}\end{align*}$$

Masukkan persamaan (2) ke persamaan (1) :

$$\begin{align*} F _{1x} &=  \frac{1}{2}\sqrt{3} F_3\\ &=  \frac{1}{2}\sqrt{3} \cdot 2mg\\ F_{1x}=F_1 &=   \sqrt{3}mg \end{align*}$$

Jawaban : A

Soal Nomor 11 : UM-UGM Fisika Tahun 2003

Balok kayu seragam di samping sepanjang 8 m dan berat 200 N berada di atas dua buah tiang penyangga A dan B. Besar beban yang dirasakan oleh titik A ( dalam N) adalah ....

A. 60

B. 90

C. 120

D. 150

E. 180

Pembahasan :

Kita tentukan poros di A :

$$\begin{align*} \Sigma \tau _B &=  0  \\ N_A \cdot 4 - w\cdot 3 &=   0 \\ 4N_A - 200\cdot 3 &=   0 \\ 4N_A - 600 &=   0 \\ 4N_A&=   600 \\ N_A &=   \frac{600}{4}\\ &=150 \quad \textrm{N}\end{align*}$$

Jawaban : D

Soal Nomor 12 : SPMB Fisika Tahun 2004

Beban bermassa 20 kg ditempatkan pada jarak 1,5 m dari kaki B (lihat gambar) pada sebuah meja datar bermassa 100 kg yang panjangnya 6 m. 

Gaya yang bekerja pada kaki A untuk menahan beban dan meja adalah ....

A. 150 N

B. 350 N

C. 550 N

D. 750 N

E. 950 N

Pembahasan :

Kita tentukan poros di B :

$$\begin{align*} \Sigma \tau _B &=  0  \\ N_A \cdot 6 - w_{meja}\cdot 3 - w_{benda}\cdot 1,5 &=   0 \\ 6N_A - 1.000\cdot 3 - 200\cdot 1,5 &=   0 \\ 6N_A - 3.000 - 300 &=   0 \\ 6N_A&=   3.300 \\ N_A &=   550 \quad \textrm{N}\end{align*}$$

Jawaban : C

Soal Nomor 13 : SPMB Fisika Tahun 2004

Suatu batang tipis dengan panjang L massa m dapat berputar pada sumbu ang terletak di ujung batang. Pada awalnya batang berada pada posisi horisontal dan kemudian dilepas. Pada saat batang membuat sudut θ dengan arah vertikal, percepatan sudut rotasi batang adalah .....

A. $\frac{g}{L}$

B. $\frac{3g\sin \theta}{2L}$

C. $\frac{6g}{L\sin \theta}$

D. $\frac{3g\cos \theta }{2L}$

E. $\frac{6g}{L\cos \theta}$

Pembahasan :

Jawaban : D