CONTOH SOAL DAN PEMBAHASAN RANGKAIAN R-L-C

Contoh soal dan pembahasan rangkaian R-L-C - Rangkaian R-L-C (Resistor, Induktor, Kapasitor) adalah salah satu topik penting dalam analisis rangkaian AC. Pemahaman tentang cara kerja rangkaian ini, terutama saat resonansi, sangat esensial bagi pelajar teknik dan fisika. Artikel ini menyajikan contoh soal dan pembahasan mengenai rangkaian R-L-C, termasuk cara menghitung impedansi, arus, dan daya dalam berbagai kondisi. Dengan pendekatan ini, diharapkan pembaca dapat lebih memahami konsep dan aplikasi praktis dari rangkaian R-L-C.

Daftar Isi

1. No. 1. Soal SNMPTN 2017/SAINTEK/133/25
2. Contoh Soal No. 2. Contoh Soal Rangkaian Seri R-L-C
3. Contoh Soal dan Pembahasan Arus Bolak Balik R-L
4. Soal R-L-C Nomor 7 : Soal UMPTN Fisika Tahun 1999

No. 1. Soal SNMPTN 2017/SAINTEK/133/25

. Sumber arus bolak-balik memiliki amplitude tegangan 200 V dan frekuensi sudut 25 Hz mengalir melalui hambatan R = 200 Ω dan kapasitor C = $\frac{100}{\pi}$ μF yang disusun seri. Kuat arus yang melalui kapasitor tersebut adalah ….

A. $\frac{1}{4}\sqrt{2}$ A

B.  $\frac{1}{2}\sqrt{2}$ A

C.  $\sqrt{2}$ A

D. 2$\sqrt{2}$ A

E. 5$\sqrt{2}$ A

Pembahasan Rangkaian R-L-C

Frekuensi sudut :

ω=2πf=2π⋅25=50π rad/s

Reaktansi Kapasitif :

X_C= $\frac{1}{\omega C}$ = $\frac{1}{50\pi  \cdot \frac{100}{\pi}\cdot 10^{-6}}$=$\frac{1.000.000}{5.000}$ = 200 Ω

Impedansi rangkaian :

 $Z=\sqrt{R^2+X_C^2}=\sqrt{R^2+X_C^2}=\sqrt{200^2+200^2}=200\sqrt{2}$ Ω

Besar arus yang mengalir :

 $I=\frac{200}{200\sqrt{2}}=\frac{1}{2}\sqrt{2}$ A

Jawaban : B

Contoh Soal No. 2. Contoh Soal Rangkaian Seri R-L-C

Rangkaian RLC dengan R = 30 ohm, L = 40 mH, dan C = 50 μF dihubungkan pada sumber listrik. Rangkaian ini akan beresonansi pada frekuensi ….

A. $\frac{10}{\pi}\sqrt{10}$ Hz

B.  $\frac{250}{\pi}\sqrt{2}$ Hz

C. 40π$\sqrt{10}$ Hz

D.$\frac{500}{\pi}\sqrt{10}$ Hz

E. 1.000 Hz

Pembahasan Soal :

Diketahui :

L = 40 mH = 40 x 10^-3 H

C = 50 μF = 50 x 10^-6 F

Syarat resonansi jika X_L = X_C

$$\begin{align*} X_L &= X_C \\ \omega L &= \frac{1}{\omega C} \\ \omega ^2 &= \frac{1}{LC} \\ (2\pi f)^2 &= \frac{1}{LC} \\ f &= \frac{1}{2\pi \sqrt{LC}} \\ &= \frac{1}{2\pi \sqrt{40\cdot 10^{-3}\cdot 50\cdot 10^{-6}}} \\ &= \frac{1}{2\pi \sqrt{2\cdot 10^{-6}}} \\ &= \frac{1.000}{2\pi \sqrt{2}} \\ &= \frac{500}{\pi \sqrt{2}} \\ &= \frac{250}{\pi }\sqrt{2} \quad \textrm{Hz} \end{align*}$$

Jawaban Contoh Soal Dan Pembahasan Rangkaian R-L-C No. 2 : B

Contoh Soal dan Pembahasan No. 3.

Perhatikan rangkaian listrik berikut ini.

R = 600 ohm, L = 2 H, dan C = 10 μF. Tegangan sesaat sumber adalah

V=100$\sqrt{2}$ sin100t volt. Besar impedansi rangkaian dan arus efektif sumber adalah ….

A. 1.000 ohm dan 0,1 A

B. 1.000 ohm dan 1 A

C. 1.000 ohm dan 0,01 A

D. 100 ohm dan 0,1 A

E. 0,1 ohm dan 1.000 A

Pembahasan Contoh Soal :

Reakstansi Induktif :

X_L=ωL=100⋅2=200 ohm

Reaktansi Kapasitif :

$X_C =\frac{1}{\omega C} = \frac{1}{100\cdot 10\cdot 10^{-6}} = 1.000$ ohm

Besar Impedansi :

$$\begin{align*} Z &= \sqrt{R^2 + (X_L - X_C)^2} \\ &= \sqrt{600^2 + (200 - 1.000)^2} \\ &= \sqrt{600^2 + (-800)^2} \\ &= 1.000 \quad \Omega \end{align*}$$

Besar arus efektif :

$$\begin{align*} I_{ef} &= \frac{I_m}{\sqrt{2}} \\ &= \frac{\frac{V}{Z}}{\sqrt{2}} \\ &= \frac{\frac{100\sqrt{2}}{1.000}}{\sqrt{2}} \\ &= 0,1 \quad \textrm{A} \end{align*}$$

Jawaban Contoh Soal RLC : A

Contoh Soal dan Pembahasan Arus Bolak Balik R-L

Soal R-L-C No. 4. Akibat pengaruh arus bolak-balik pada rangkaian R-L seri, diperoleh data yang tertera pada gambar di bawah ini.

Berdasarkan data tersebut maka nilai reaktansi induktornya adalah ….

A. 60 ohm

B. 75 ohm

C. 120 ohm

D. 140 ohm

E. 180 ohm

Pembahasan :

$$\begin{align*} V &= I\cdot R \\ 80 &= I \cdot 100 \\ I &= \frac{80}{100} \\ &= 0,8 \quad \textrm{A} \end{align*}$$

Besar tegangan pada induktor :

$$\begin{align*} V &= \sqrt{V_R^2 + V_L^2} \\ 100 &= \sqrt{80^2 + V_L^2} \\ 100 &= \sqrt{6400 + V_L^2} \\ 10.000 &= 6.400 +V_L^2 \\ 3.600 &= V_L^2 \\ V_L &= 60 \quad \textrm{V} \end{align*}$$

Nilai reaktansi induktornya:

$$\begin{align*} V_L &= I\cdot X_L \\ 60 &= 0,8\cdot X_L \\ X_L &= \frac{60}{0,8} \\ &= 75 \quad \textrm{ohm} \end{align*}$$

Jawaban : B

Contoh Soal dan Pembasahan RLC No. 5

Rangkaian resistor pada tegangan bolak balik menghasilkan beda fase antara arus dan tegangan sebagai berikut ….

A. Arus terlambat 90^o terhadap tegangan

B. Arus mendahului 90^o terhadap tegangan

C. Arus dan tegangan berbeda fase 0^o

D. Arus mendahului 180^o terhadap tegangan

E. Arus terhambat 180^o terhadap tegangan

Jawaban : C

Soal No. 5 Soal SPMB tahun 2014/IPA/39 tentang RLC

Sumber DC 2 volt dihubungkan dengan 2 elemen listrik yang dipasang seri dan arus yang mengalir pada rangkaian tersebut 200 mA. Jika sumber DC diganti dengan AC 2 volt ( 50 Hz ) maka arus yang mengalir pada rangkaian menjadi 100 mA. Komponen listrik pada rangkaian ini adalah ….

A. kapasitor 20 F dan resistor 10 Ω

B. Induktor  $\frac{\sqrt{3}}{10\pi}$ H dan kapasitor 20 F

C. resistor 10 Ω dan induktor $\frac{\sqrt{3}}{10\pi}$ H

D. dua-duanya resistor, masing-masing 10 Ω

E. dua-duanya induktor, masing-masing $\frac{\sqrt{3}}{10\pi}$ H

Pembahasan :

Diketahui :

V_DC = 2 volt; I_DC= 200 mA = 0,2 A

V_AC= 2 volt; I_AC= 100 mA = 0,1 A

f = 50 Hz

Arus DC yang mengalir, maka elemen yang mungkin adalah resistor dan induktor. Hambatan pada induktor jika menggunakan sumber tegangan DC adalah nol.

$$\begin{align*} V_{DC} &= I_{DC}\cdot R_{DC} \\ 2 &= 0,2\cdot R_{DC} \\ R_{DC} &= \frac{2}{0,2} \\ &= 10 \quad \textrm{ohm} \end{align*}$$

Dihubungkan dengan sumber AC 2 volt, arus yang mengalir = 100 mA = 0,1 A

$$\begin{align*} V_{AC} &= I_{AC}\cdot Z \\ 2 &= 0,1\cdot Z \\ Z &= 20 \quad \textrm{ohm} \end{align*}$$

Kemudian dicari reaktansi induktifnya :

$$\begin{align*} Z &= \sqrt{R^2 + X_L^2} \\ 20 &= \sqrt{10^2 + X_L^2} \\ 400 &= 100 + X_L^2 \\ 300 &= X_L^2 \\ X_L &= 10\sqrt{3} \quad \textrm{ohm} \end{align*}$$

Kemudian mencari besar induktornya :

$$\begin{align*} X_L &= \omega \cdot L \\ 10\sqrt{3} &= 2\pi f \cdot L \\ 10\sqrt{3} &= 2\pi \cdot 50 \cdot L \\ 10\sqrt{3} &= 100\pi \cdot L \\ L &= \frac{10\sqrt{3}}{100\pi } \\ &= \frac{\sqrt{3}}{10\pi } \quad \textrm{H} \end{align*}$$

Jawaban Pembahasan Soal R-L-C SPMB tahun 2014 : C

Soal No. 6 Soal SBMPTN tahun 2014

Sebuah pemancar radio dioperasikan pada frekuensi 1 MHz dengan rangkaian osilasi mempunyai kapasitansi 200 pF. Besar induktansi rangkaian tersebut adalah ….

A. 140 μH

B. 127 μH

C. 114 μH

D. 101 μH

E. 88 μH

Pembahasan Soal RLC SBMPTN tahun 2014 :

Diketahui:

f = 1 MHz = 1 x 10⁶ Hz

C = 200 pF = 200 x 10^-12 F = 2 x 10^-10 F

Pada pemancar radio mengalami resonansi sehingga :

$$\begin{align*} X_L &= X_C \\ \omega L &= \frac{1}{\omega C} \\ \omega ^2 &= \frac{1}{LC} \\ (2\pi f)^2 &= \frac{1}{LC} \\ f &= \frac{1}{2\pi \sqrt{LC}} \\ 1\cdot 10^6 &= \frac{1}{2\pi \sqrt{L \cdot 2\cdot 10^{-10}}} \\ 1\cdot 10^{12}&= \frac{1}{4\pi ^2 \cdot 2\cdot 10^{-10} \cdot L} \\ 1\cdot 10^{12}&= \frac{1}{8\pi ^2 \cdot 10^{-10} \cdot L} \\ 8\pi ^2 \cdot 10^{2} \cdot L&= 1 \\ L&= \frac{1}{8\pi ^2 \cdot 10^{2}} \\ &= 1,27 \cdot 10^{-4} \quad \textrm{H}\\ &= 127 \cdot 10^{-6} \quad \textrm{H}\\ &= 127 \quad \mu\textrm{H}\\ \end{align*}$$

Jawaban : B

Soal R-L-C Nomor 7 : Soal UMPTN Fisika Tahun 1999

Suatu rangkaian seri R-L-C dipasang pada tegangan listrik bolak-balik yang nilai efektifnya 100 V dan frekuensinya 60 Hz. Bila R = 10 ohm, L = 25,5 mH dan C = 106 μF maka beda potensial (tegangan) dalam volt antara ujung-ujung L adalah ....

A. 5,56

B. 100

C. 55,6

D. 556

E. 60

Pembahasan soal R-L-C nomor 6 :

Frekuensi sudut :

$$\begin{align*} \omega &= 2\pi f \\ &= 2\cdot 3,14 \cdot 60 \\ &= 376,8 \quad \textrm{rad/s} \end{align*}$$

Reaktansi induktif :

$$\begin{align*} X_L &= \omega \cdot L \\ &= 367,8 \cdot 26,5 \cdot 10^{-3} \\ &= 10 \quad \textrm{ohm} \end{align*}$$

Reaktansi kapasitif :

$$\begin{align*} X_C &= \frac{1}{\omega C} \\ &= \frac{1}{367,8\cdot 106\cdot 10^{-6}} \\ &= \frac{1}{3,89 \cdot 10^{-2}} \\ &= 25 \quad \textrm{ohm} \end{align*}$$

Impedansi :

$$\begin{align*} Z &= \sqrt{R^2 + (X_L - X_C)^2} \\ &= \sqrt{10^2 +(10 - 25)^2} \\ &= \sqrt{10^2 +(-15)^2} \\ &= \sqrt{100 +225} \\ &= \sqrt{325} \\ &= 18 \quad \textrm{ohm} \end{align*}$$

Arus pada rangkaian :

$$\begin{align*} V &= I \cdot Z \\ 100 &= I \cdot 18 \\ I &= 5,56 \quad \textrm{A} \end{align*}$$

Beda potensial pada ujung-ujung induktor :

$$\begin{align*} V_L &= I \cdot X_L \\ &= 5,56 \cdot 10 \\ I &= 55,6 \quad \textrm{volt} \end{align*}$$

Jawaban soal R-L-C nomor 6: C

Soal R-L-C Nomor 7 : Soal SPMB Fisika Tahun 2002

Diketahui bahwa arus listrik searah (DC) sebesar 3 ampere yang mengalir melewati suatu filamen pemanas mampu menghasilkan daya listrik padanya sebesar W. Kalau digunakan arus bolak-balik (AC) dengan nilai puncak sebesar 3 ampere juga maka besar daya listrik sekarang yang dapat dibangkitkan pada filamen adalah ....

A. W/4

B. W/2

C. 2W

D. 4W

E. W

Pembahasan soal :

Daya pada arus searah (DC) :

$$\begin{align*} P_{DC} &= I_{DC}^2\cdot R \\ W &= 3^2 \cdot R \\ R &= \frac{W}{9} \end{align*}$$

Daya pada arus bolak-balik (AC) :

$$\begin{align*} P_{AC} &= I_{ef}^2\cdot R \\ &= \left(\frac{I_{maks}}{\sqrt{2}} \right)^2\cdot R \\ &= \left( \frac{3}{\sqrt{2}}\right)^2\cdot \frac{W}{9} \\ &= \frac{9}{2} \cdot \frac{W}{9} \\ &= \frac{W}{2} \end{align*}$$

Jawaban soal R-L-C Nomor 7 : B

Soal Nomor 8 : UM-UGM Fisika Tahun 2004

Dalam suatu untau RLC ideal yang terpasang seri dengan tegangan listrik AC 

A. semua daya terdisipasi dalam induktor L

B. semua daya terdisipasi dalam resistor R

C. semua daya terdisipasi dalam kapasitor C

D. daya terdisipasi baik dalam kapasitor, induktor maupun resistor secara sama

E. daya terdisipasi dalam ketiga elemen RLC dalam proporsi berbeda yang sebanding lurus dengan nilai impedansi R, L, dan C

Pembahasan :

P_AC = V_ef  x I_ef  x cos α = I_ef² x R ← (R L C seri = arus sama)

Daya akan terdisipasi pada resistor R

Jawaban : B

Soal Nomor 9 : UM-UGM Fisika tahun 2006

Sebuah induktor dan kapasitor masing-masing dengan induktansi dan kapasitansi 20 μH dan 4 F dihubungkan secara seri dengan generator 60 Hz, 120 V AC. Besar beda potensial pada ujung-ujung induktor 20  μH adalah sekitar ....

A. 84 V

B. 108 V

C. 132 V

D. 144 V

E. 160 V

Pembahasan :

Frekuensi sudut :

$\omega = 2\pi f = 2 \cdot 3,14 \cdot 60 = 376,8$ rad/s

Reaktansi Kapasitif :

$X_C = \frac{1}{\omega C} =\frac{1}{376,8 \cdot 4} = \frac{1}{1.507,2} = 6,63 \cdot 10^{-4}$ ohm

Reaktansi Induktif :

$X_L = \omega L = 376,8 \cdot 20 \cdot 10^{-6} = 7536 \cdot 10^{-6} = 75,36 \cdot 10^{-4}$ ohm

Impedansi :

$$\begin{align*} Z &= \sqrt{R^2 + (X_L - X_C)^2} \\ &= \sqrt{0^2 +(X_L - X_C)^2} \\ &= \sqrt{(X_L - X_C)^2} \\ &= X_L - X_C \\ &= 75,36\cdot 10^{-4} - 6,63\cdot 10^{-4} \\ &= 68,73 \cdot 10^{-4} \quad \textrm{ohm} \end{align*}$$

Arus pada rangkaian :

$$\begin{align*} V &= I\cdot Z \\ 120 &= I\cdot 68,73\cdot 10^{-4} \\ I &= 17.459,624 \quad \textrm{A} \end{align*}$$

Tegangan pada induktor :

$$\begin{align*} V_L &= I\cdot X_L \\ &= 17.459,624 \cdot 75,36\cdot 10^{-4} \\ &= 132 \quad \textrm{volt} \end{align*}$$

Jawaban : C

Soal Nomor 10 : 

Kita ukur tegangan jaringan listrik di rumah dengan memakai volmeter, maka yang terukur adalah tegangan ....

A. maksimumnya

B. efektifnya

C. sesaatnya

D. rata-ratanya

E. minimumnya

Pembahasan :

Tegangan yang terukur dengan volmeter adalah tegangan efektif. Perhatikan, tegangan maksimum tidak bisa diukur oleh volmeter. Tegangan maksimum hanya bisa diperoleh dengan melihat grafik tegangan ac pada osiloskop.

Jawaban : B

Soal Nomor 11 Rangkaian R-L-C :

Jarum suatu volmeter yang dipergunakan untuk mengukur suatu tegangan bolak-balik menunjukkan harga 110 volt. Ini berarti behwa tegangan itu :

A. tetap

B. berubah antara 0 dan 110 volt

C. berubah antara 0 dan 110 volt

D. berubah antara -110 volt dan +110 volt

E. berubah antara -110 dan +110 volt

Pembahasan :

Voltmeter menunjukkan 110 volt artinya V_ef = 110 volt. Bentuk tegangan ac dan persamaannya adalah V = V_m sin ωt dengan tegangan maksimum V_m = V_ef$\sqrt{2}$ 

V_m = 110$\sqrt{2}$ volt, sehingga V =110$\sqrt{2}$ sin ωt, ini berarti tegangan berubah antara  -110$\sqrt{2}$ volt dan +110$\sqrt{2}$ volt

Jawaban : E

Soal Nomor 12

Dalam rangkaian seri (R = 60 ohm) dan konduktor dalam tegangan arus bolak-balik, kuat arus yang lewat 2 A. Jika dalam diagram vektor di bawah ini tan α = 3/4 maka tegangan induktor ....

A. 72 V

B. 90 V

C. 120 V

D. 160 V

E. 200 V

Pembahasan :

$$\begin{align*} \tan \alpha &= \frac{X_L}{R}\\ \frac{3}{4} &= \frac{X_L}{60}\\ X_L &= 45 \quad \textrm{ohm} \end{align*}$$

Tegangan induktor :

$$\begin{align*} V_L &= I\cdot X_L\\ &= 2\cdot 45\\ &= 90 \quad \textrm{V} \end{align*}$$

Jawaban : B

Soal Nomor 13

Tegangan suatu sumber AC tampak pada layar osiloskop seperti gambar di bawah ini. Tombol tegangan pada osiloskop menunjuk pada posisi 50 V/skala. Jika √2 = 1,4 dan tegangan tersebut diukur dengan voltmeter AC, hasilnya adalah ....

A. 14,28 volt

B. 35,7 volt 

C. 50 volt

D. 142 volt

E. 280 volt

Pembahasan :

Dari layar osilokop diperoleh tegangan maksimum :

V_m = 50 V/skala x 4 skala = 200 volt

Tegangan yang diukur voltmeter adalah tegangan efektifnya :

$$\begin{align*} V_{ef} &= \frac{V_m}{\sqrt{2}}\\ &= \frac{200}{1,4}\\ &= 142 \quad \textrm{V} \end{align*}$$

Jawaban : D

Soal Nomor 14

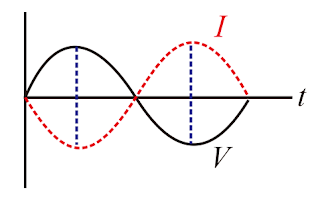
Grafik berikut yang menggambarkan hubungan I dan V terhadap untuk induktor yang dialiri arus adalah ....

A.
B.
C.
D.
E.

Pembahasan :

Untuk induktor yang dialiri arus maka rangkaian bersifat Induktif yaitu arus tertinggal 90 derajat dibanding tegangan.

Arus: Tertinggal di belakang tegangan, ditandai dengan sudut fasa positif.

Tegangan pada Induktor: Mendahului arus, mendominasi karena X_L > X_C

Jawaban : D

Soal Nomor 15 Rangkaian R-L-C

Penunjukan ammeter A adalah 2 mA dan penunjukan voltmeter V adalah 30 volt. Berarti frekuensi arus AC dalam rangkaian tersebut adalah....

A. 25 Hz

B. 50 Hz

C. 100 Hz

D. 500 Hz

E. 1.000 Hz

Pembahasan :

Reaktansi Kapasitif :

$$\begin{align*} V_{C} &= I\cdot X_C\\ 20 &= 2\cdot 10^{-3}\cdot X_C\\ X_C &= 10.000 \quad \textrm{ohm} \end{align*}$$

Frekuensi rangkaian :

$$\begin{align*} X_{C} &= \frac{1}{\omega C}\\ 10.000 &= \frac{1}{\omega C}\\ \omega C &= 1\cdot 10^{-4} \\ 2\pi f \cdot \frac{2}{\pi} \cdot 10^{-6} &= 1\cdot 10^{-4} \\ f &=25 \quad \textrm{Hz} \end{align*}$$

Jawaban : A

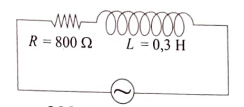
Soal Nomor 16 R-L-C

Jika frekuensi anguler sumber tegangan 2.000 rad/s maka impedansi rangkaian pada gambar berikut adalah ....

A. 300 ohm

B. 500 ohm

C. 640 ohm

D. 830 ohm

E. 1.000 ohm

Pembahasan :

Reaktansi Induktif :

$X_L = \omega L =0,3\cdot 2000 = 600$ ohm

Impedansi rangkaian :

$$\begin{align*} Z &= \sqrt{R^2 + X_L^2}\\ &= \sqrt{800^2 + 600^2}\\ &= \sqrt{1.000^2}\\ &= 1.000 \quad \textrm{ohm} \end{align*}$$

Jawaban : E

Soal R-L-C Nomor 17

Rangkaian seri pada gambar di bawah ini memiliki impedansi minimum jika R = 100 ohm, L = 0,1 H, dan C = $\frac{1}{1.000\pi ^2}$  F. Frekuensi tegangan bolak-balik yang terpasang adalah ....

A. 10π Hz

B. 25π Hz

C. 50 Hz

D. 100 Hz

E. 150 Hz

Pembahasan :

Impedansi minimum terjadi saat Z = R, sehingga X_L = X_C, maka :

$$\begin{align*} X_L &= X_C \\ \omega L &= \frac{1}{\omega C} \\ \omega ^2 &= \frac{1}{LC} \\ (2\pi f)^2 &= \frac{1}{LC} \\ f &= \frac{1}{2\pi \sqrt{LC}} \\ &= \frac{1}{2\pi \sqrt{0,1 \cdot \frac{1}{1.000\pi ^2}}} \\ &= \frac{1}{2\cdot 10^{-2}} \\ &= 50 \quad \textrm{Hz}\\ \end{align*}$$

Jawaban : C

Soal R-L-C Nomor 18 :

Kuat arus yang mengalir pada induktor dengan induktansi diri 0,5 henry yang dihubungkan ke sumber tegangan bolak-balik 220 volt, 50 Hz adalah ....

A. $\frac{1}{5}\pi$ A

B.  $\frac{2}{\pi}$ A

C.  $1\frac{1}{5}\pi$ A

D. $\frac{22}{5\pi}$ A

E.  $\frac{22}{\pi}$A

Pembahasan :

Frekuensi angular :

$\omega = 2\pi f = 2\pi \cdot 50 = 100\pi$ rad/s

Reaktansi Induktif :

$X_L = \omega L = 100\pi \cdot 0,5 = 50\pi$ ohm

Arus pada induktor :

$$\begin{align*} I &= \frac{V}{X_L}\\ &= \frac{220}{50\pi}\\ &= \frac{22}{5\pi} \quad \textrm{A} \end{align*}$$

Jawaban Rangkaian R-L-C : D

Soal R-L-C Nomor 19 :

Perhatikan rangkaian listrik berikut ini.

Jika kuat arus dalam rangkaian 4 A, nilai resistor R pada rangkaian adalah ....

A. 60 ohm

B. 50 ohm

C. 40 ohm

D. 30 ohm

E. 20 ohm

Pembahasan :

Frekuensi angular :

$\omega = 2\pi f = 2\pi \cdot \frac{50}{\pi} = 100$ rad/s

Reaktansi Kapasitif :

$X_C = \frac{1}{\omega C} = \frac{1}{100\cdot 250 \cdot 10^{-6}} = 40$ ohm

Impedansi:

$$\begin{align*} V &= I\cdot Z\\ 200 &= 4\cdot Z\\ Z &= 50 \quad \textrm{ohm} \end{align*}$$

Kemudian mencari hambatan resistor :

$$\begin{align*} Z &= \sqrt{R^2 +X_C^2}\\ 50 &= \sqrt{R^2 +40^2}\\ 2.500 &= R^2 +1.600\\ R^2 &= 900\\ R &= 30 \quad \textrm{ohm} \end{align*}$$

Jawaban : D

Soal R-L-C Nomor 20 :

Suatu rangkaian seri resistor 20 ohm dan kapasitor 2 μF dihubungkan ke sumber arus bolak-balik dengan frekuensi 200 rad/s. Besar induktansi induktor yang harus di pasang seri dengan rangkaian agar terjadi resonansi adalah ...

A. 5 H

B. 7,5 H

C. 8 H

D. 10 H

E. 12,5 H

Pembahasan :

Resonsansi terjadi ketika X_L = X_C,

$$\begin{align*} X_L &= X_C \\ \omega L &= \frac{1}{\omega C} \\ \omega ^2 &= \frac{1}{LC} \\ 200^2 &= \frac{1}{L\cdot 2\cdot 10^{-6}} \\ 8\cdot 10^{-2} L &= 1 \\ L&= \frac{1}{8\cdot 10^{-2}}\\ &= 12,5 \quad \textrm{H}\\ \end{align*}$$

Jawaban : E

Soal R-L-C Nomor 21 :

Rangkaian seri terdiri atas hambatan murni 200 ohm, kumparan dengan induksi diri 0,8 henry dan kapasitor dengan kapasitas 8 μF dipasang pada tegangan 200 volt dengan frekuensi anguler 500 rad/s. Besarnya kuat arus dalam rangkaian tersebut adalah .... 

A. 0,57 A

B. 0,80 A

C. 1,00 A

D. 1,25 A

E. 1,33 A

Pembahasan :

Reaktansi Induktif:

$X_L =\omega L = 500\cdot  0,8 = 400$ ohm

Reaktansi Kapasitif :

$X_C = \frac{1}{\omega C} = \frac{1}{500\cdot 8 \cdot 10^{-6}} = 250$ ohm

Impedansi rangkaian :

$$\begin{align*} Z &= \sqrt{R^2+(X_L^2 - X_C^2)} \\ &= \sqrt{200^2+(400- 250)^2} \\ &= \sqrt{200^2+ 150^2} \\ &= \sqrt{62.500} \\ &= 250 \quad \textrm{ohm}\\ \end{align*}$$

Arus pada rangkaian :

$$\begin{align*} V &= I\cdot Z \\ 200 &= I\cdot 250 \\ I &= 0,8 \quad \textrm{A}\\ \end{align*}$$

Jawaban : B

Soal R-L-C Nomor 22

Dalam suatu untai RLC ideal yang terpasang seri dengan sumber AC, pada saat terjadi resonansi

1. beda sudut fase antara arus dan tegangan sama dengan nol;

2. impedansi rangkaian = R;

3. arus efektif pada rangkaian bernilai maksimum;

4. semua daya terdisipasi dalam resistor. 

Pernyataan di atas yang benar adalah ....

A. 1, 2, dan 3 

B. 1 dan 3

C. 2 dan 4

D. 4 saja

E. 1, 2, 3, dan 4

Pembahasan :

Dalam sebuah rangkaian RLC seri dengan sumber AC, resonansi terjadi ketika frekuensi sumber AC sama dengan frekuensi resonansi dari rangkaian. Pada kondisi resonansi, beberapa karakteristik unik terjadi:

Beda sudut fase antara arus dan tegangan sama dengan nol (0°):

Pada resonansi, reaktansi induktif (X_L) sama dengan reaktansi kapasitif (X_C), sehingga mereka saling meniadakan. Ini membuat impedansi total rangkaian menjadi resistif murni, sehingga arus dan tegangan berada dalam fase yang sama. Oleh karena itu, beda sudut fase antara arus dan tegangan adalah nol.

Impedansi rangkaian sama dengan R:

Karena X_L dan X_C saling meniadakan, impedansi total rangkaian hanya terdiri dari resistansi R. Jadi, impedansi efektif rangkaian pada resonansi sama dengan R.

Arus efektif pada rangkaian bernilai maksimum:

Dengan impedansi yang hanya berupa R dan tidak adanya komponen reaktansi (induktif atau kapasitif) yang memberikan hambatan tambahan, arus yang mengalir pada rangkaian akan mencapai nilai maksimumnya karena tidak ada hambatan reaktif.

Semua daya terdisipasi dalam resistor:

Pada resonansi, karena impedansi total adalah resistif murni, semua daya yang diserap oleh rangkaian akan terdisipasi sebagai panas dalam resistor. Tidak ada daya yang disimpan dalam komponen reaktif (induktor atau kapasitor).

Berdasarkan penjelasan di atas, pernyataan yang benar adalah:

Jawaban : E. 1, 2, 3, dan 4