HUKUM NEWTON CONTOH SOAL DAN PEMBAHASAN

Hukum Newton contoh soal dan pembahasan – Hukum Newton ada tiga yaitu Hukum Newton 1, Hukum Newton 2 dan Hukum Newton 3. Hukum Newton banyak aplikasinya dalam kehidupan sehari-hari dan dalam dunia teknologi modern ada banyak penerapan Hukum Newton.

Hukum Newton Dan Rumusnya

Rumus Hukum Newton di bagi tiga yaitu :

Hukum I Newton

Hukum I Newton  membahas tentang kelembamam benda. Hukum I Newton atau hukum kelembamam menyatakan bahwa jika resultan haya yang bekerja pada suatu benda sama dengan nol, benda yang diam akan tetap diam dan benda yang bergerak dengan kecepatan konstan akan tetap bergerak dengan kecepatan konstan. Sehingga Hukum Newton 1 dirumuskan :

ΣF=0

Hukum II Newton

Hukum II Newton menyatakan bahwa percepatan pada suatu benda berbanding lurus dengan gaya yang bekerja pada benda tersebut dan bebanding terbalik dengan massa benda tersebut.

$a= \frac{\Sigma F}{\Sigma m}$

Hukum III Newton

Hukum III Newton menyatakan bahwa jika benda A melakukan gaya aksi pada benda B, benda B akan memberikan gaya reaksi yang sama besar, tetapi berlawanan pada benda A.

ΣF_aksi=−ΣF_reaksi

_{{tocify} $title={Custom Title}}

Contoh Soal Dan Pembahasan Fisika Hukum Newton 1

Sebuah balok bermassa 4 kg berada di atas bidang miring kasar seperti gambar berikut.

Besar gaya minimum yang diperlukan agar balok meluncur ke bawah dengan kecepatan tetap adalah ….

A. 3,2 N

B. 6,4 N

C. 20,8 N

D. 32 N

E. 48 N

Pembahasan contoh soal hukum newton pada bidang miring :

Perhatikan gambar gaya-gaya yang bekerja pada benda berikut ini :

Besar gaya berat (w) :

w = mg = 4⋅10 = 40N

w_x = wsin37^o = 40⋅0,6 = 24 N

w_y = wcos37^o = 40⋅0,8 = 32 N

Komponen sumbu Y :

Sepanjang sumbu y berlaku hukum I Newton sehingga : 

$$\begin{align*} \Sigma F_y &= 0 \\ N - w_y &= 0 \\    N &= w_y \\&= 32 \quad \textrm{N}\end{align*}$$

Komponen sumbu X :

Agar balok meluncur ke bawah dengan kecepatan tetap maka berlaku Hukum I Newton :

$$\begin{align*} \Sigma F_x &= 0 \\ f + F_x - w_x &= 0 \\    f &= w_x - F_x \\\mu N &= w_x - F_x \\0,1 \cdot 32 &= 24 - F_x\\F_x &= 24 - 3,2  \\&= 20,8 \quad \textrm{N}\end{align*}$$

Jawaban contoh soal hukum newton pada bidang miring : C

Hukum Newton Berkaitan Dengan Gerak Benda

Contoh soal hukum newton berkaitan dengan gerak benda :

Sebuah benda bermassa 1 kg mula-mula bergerak mendatar dengan kecepatan 10 m/s. Kemudian, diberi gaya konstan 2 N selama 10 s searah dengan arah gerak. Besar kecepatan benda setelah 10 s tersebut adalah ….

A. 15 m/s

B. 20 m/s

C. 25 m/s

D. 30 m/s

E. 35 m/s

Pembahasan hukum newton berkaitan dengan gerak benda :

Untuk menentukan percepatan benda mengunakan Hukum II Newton :

$$\begin{align*} a &= \frac{\Sigma F}{m} \\ &= \frac{2}{1} \\   &= 2 \quad \textrm{m/s}^2\end{align*}$$

Kemudian menggunakan persamaan gerak benda yang dipercepat (GLBB) :

$v_t = v_o + at = 10 + 2\cdot 10 = 10 +  20 = 30$ m/s

Jawaban hukum newton berkaitan dengan gerak benda : D

Hukum Newton Pada Katrol

Contoh soal hukum newton pada katrol :

Dua benda, m₁ dan m₂, bermassa masing-masing 4 kg dan 6 kg dihubungkan dengan seutas tali melalui sebuah katrol yang massanya diabaikan seperti gambar berikut.

Percepatan dan tegangan talinya adalah ….

A. 10 m/s², 60 N

B. 10 m/s², 40 N

C. 10 m/s², 20 N

D. 2 m/s², 48 N

E. 2 m/s², 24 N

Pembahasan hukum newton pada katrol :

Perhatikan diagram gaya yang bekerja pada katrol berikut :

Hukum II Newton pada sistem benda 1 :

$$\begin{align*} \Sigma F_y &= m_1 a \\ T_1 - w_1 &= m_1 a \\ T_1 - m_1 g &= m_1 a \\ T_1 - 4\cdot 10 &= 4 a \\ T_1 - 40 &= 4 a \\ T_1 &= 40 + 4a \quad \textrm{ ............................ (1)} \end{align*}$$

Hukum II Newton pada sistem benda 2 :

$$\begin{align*} \Sigma F_y &= m_2 a \\ T_2 - w_2 &= m_2(- a) \\ T_2 - m_2 g &= -m_2 a \\ T_2 - 6\cdot 10 &= -6 a \\ T_2 - 60 &= -6a \\ T_2 &= 60 - 6a \quad \textrm{ ............................ (2)}\end{align*}$$

Karena massa katrol diabaikan maka T₁ = T₂, sehingga :

$$\begin{align*} T_1 &= T_2 \\ 40 + 4a &= 60 - 6a \\ 4a + 6a &= 60 - 40 \\ 10a &= 20 \\ a &= 2 \quad \textrm{ m/s}^2 \end{align*}$$

Jadi percepatan benda a = 2 m/s².

Untuk menentukan besar tegangan talinya bisa menggunakan salah satu T₁ atau T₂, besar keduanya sama.

$T_1 = 40 + 4a = 40 + 4\cdot 2 = 40 + 8 = 48$ N

Atau menggunakan T₂ , sehingga :

$T_2 = 60 - 6a = 60 - 6\cdot 2 = 60  - 12 = 48$ N

Jadi besar tegangan talinya 48 N.

Jawaban hukum newton pada katrol : D

Aplikasi hukum newton pada bidang miring

Contoh aplikasi Hukum Newton pada bidang miring adalah sebagai berikut :

Sebuah benda bermassa 5 kg ditarik ke atas dari keadaan diam dengan gaya 70 N seperti gambar.

Jika koefisien gesekan bidang miring (μ_k = 0,2), percepatan benda adalah ….

A. 32 m/s²

B. 8 m/s²

C. 6,4 m/s²

D. 3 m/s²

E. 1,5 m/s²

Pembahasan aplikasi Hukum Newton pada bidang miring :

Perhatikan diagram gaya berikut ini :

Diketahui :

F = 70 N

w = 5 x 10 = 50 N

w_x= w x sin 37 = 50 x 0,6 = 30 N

w_y= w x cos 37 = 50 x 0,8 = 40 N

Komponen sumbu y berlaku Hukum I Newton :

$$\begin{align*} \Sigma F_y &= 0 \\ N - w_y &= 0 \\ N &= w_y \\  &= 40 \quad \textrm{N}\end{align*}$$

Komponen sumbu x berlaku Hukum II Newton :

$$\begin{align*} \Sigma F_x &=ma \\ F - w_x - f_g &= ma \\ F - w_x - \mu N &= ma \\ 70 - 30 - 0,2\cdot 40 &= 5a \\ 40 - 8 &= 5a \\ 5a &= 32 \\  &= 6,4 \quad \textrm{m/s}^2\end{align*}$$

Jawaban aplikasi Hukum Newton pada bidang miring : C

Contoh Soal Dan Pembahasan Penerapan Hukum Newton Pada Bidang Datar

Contoh soal dan pembahasan serta penerapan hukum newton pada bidang datar baik licin maupun kasar.

Contoh soal :

Sebuah balok bermassa 2 kg yang terletak pada bidang datar licin ditarik dengan gaya F₁ dan F₂ seperti gambar berikut.

Besar dan arah percepatan yang bekerja pada benda adalah ….

A. 1,25 m/s² ke kiri

B. 1,25 m/s² ke kanan

C. 0,8 m/s² ke kiri

D. 0,8 m/s² ke kanan

E. 0,5 m/s² ke kiri

Pembahasan penerapan hukum newton pada bidang datar :

Perhatikan diagram gaya berikut :

F_2x = F₂ cos 37 = 8 x 0,8 = 6,4 N

F_2y = F₂ sin 37 = 8 x 0,6 = 4,8 N

Benda bergerak sepanjang bidang datar sumbu x, sehingga berlaku Hukum II Newton.

$$\begin{align*} \Sigma F_x &= ma \\ F_{2x} - F_1 &= ma \\ 6,4 - 8 &= 2a \\ -1,6 &= 2a \\ a &= -0,8 \quad \textrm{m/s}^2\end{align*}$$

Karena percepatan (a) negatif, maka benda bergerak sepanjang bidang datar ke kiri.

Jawaban : E

Contoh soal dan pembahasan hukum newton 3

Hukum Newton 3 tentang aksi reaksi, berikut ini contoh soal tentang hukum 3 newton dan pembahasannya:

Perhatikan gambar berikut.

Pasangan gaya aksi dan reaksi adalah ….

A. T₁ dan w

B. T₁ dan T₂

C. T₁ dan T₃

D. T₂ dan T₁

E. T₂ dan T₃

Pembahasan contoh soal Hukum 3 Newton :

Pasangan gaya aksi dan reaksi bekerja pada benda yang berbeda dan beralawan arah. T₁ dan w bukan pasangan aksi reaksi karena bekerja pada benda yang sama yaitu benda yang mengantung. Begitu juga T₂ dan T₃ bukan pasangan aksi reaksi karena bekerja pada benda yang sama yaitu langit-langit. Sehingga yang merupakan pasangan gaya aksi dan reaksi adalah T₁ dan T₂, karena T₁ bekerja pada benda yang menggantung dan T₂ bekerja pada langit-langit dan keduannya berlawanan arah.

Jawaban : B

Artikel ini berkaitan dengan hukum newton ketiga, hukum newton tentang gaya, hukum newton pertama, hukum newton aksi reaksi, hukum newton katrol, hukum newton 1 membahas tentang, hukum newton 3 adalah, hukum newton contoh soal, hukum newton 2 dan aplikasinya, hukum newton dan aplikasinya, peristiwa hukum newton alasan, aplikasi hukum newton 1, aplikasi hukum newton 2, artikel hukum newton, aplikasi hukum newton 1 2 3, animasi hukum newton 1, aplikasi hukum newton 3, dan aplikasi hukum newton pada bidang datar.

Contoh soal dan pembahasan hukum newton tentang Lift

Seorang anak bermassa 60 kg ditimbang dalam lift yang sedang bergerak, ternyata jarum timbangan menunjukkan angka 900 N. Jika percepatan gravitasi 10 m/s² dapat disimpulkan bahwa ....

A. massa anak dalam lift 90 kg 

B. lift sedang bergerak ke atas dengan kecepatan tetap 

C. lift sedang bergerak ke bawah dengan percepatan tetap 

D. lift sedang bergerak ke atas dengan percepatan tetap 

E. lift sedang bergerak ke bawah dengan kecepatan tetap

Pembahasan :

$$\begin{align*} \Sigma F_x &= ma \\ N - w &= ma \\ N - mg &= ma \\ 900 - 60\cdot 10 &= 60a \\ 900 - 600 &= 60a \\  300 &= 60a \\ a &=\frac{300}{60} \\a &= 5 \quad \textrm{m/s}^2 \end{align*}$$

Karena percepatan a = 5 m/s², maka benda sedang bergerak ke atas dengan percepatan tetap.

Jawaban : D

Contoh Soal Hukum II Newton

Benda bermassa 50 kg bergerak dengan kecepatan 4 m/s. Besar gaya yang diperlukan untuk menghentikan setelah menempuh jarak 10 m benda adalah ....

A. 0,8 N 

B. 10 N

C. 20 N

D. 40 N 

E. 80 N

Pembahasan :

Perlambatan benda :

$$\begin{align*} v_t^2 &= v_o^2 -2as \\ 0^2 &= 4^2 -2\cdot a \cdot 10 \\ 0 &= 8 - 20a \\ 20a &= 8 \\ a &= \frac{8}{20} \\  &= 0,4 \quad \textrm{m/s}^2 \end{align*}$$

Besar gaya yang diperlukan :

$$\begin{align*} \Sigma F &= ma \\ F &= 50\cdot 0,4 \\ &= 20 \quad \textrm{N} \end{align*}$$

Jawaban : C

Contoh Soal Nomor 1

Sebuah benda berada di atas bidang datar yang licin. Jika pada benda bekerja gaya mendatar 10 N, timbul percepatan 5 m/s². Jika gaya mendatar tersebut diubah menjadi 15 N, percepatan benda menjadi ....

A. 1 m/s²

B. 2,5 m/s²

C. 3 m/s²

D. 7,5 m/s²

E. 10 m/s²

Pembahasan :

$$\begin{align*} m &= m' \\ \frac{F}{a} &= \frac{F'}{a'} \\ \frac{10}{5} &= \frac{15}{a'} \\ 2 &= \frac{15}{a'} \\ a' &= 7,5 \quad \textrm{m/s}^2 \end{align*}$$

Jawaban : D

Contoh Soal Nomor 2

Dua benda yang bermassa masing-masing 2 kg dan 1 kg dihubungkan dengan tali dan ditarik oleh gaya tetap 24 N. 

Besar tegangan tali penghubung kedua benda adalah .... 

A. 8 N

B. 10 N 

C. 12 N 

D. 15 N 

E. 16 N 

Pembahasan :

Komponen gaya yang bekerja pada benda 1 :

$$\begin{align*} \Sigma F &= ma \\ T &=m_1 a \\ &= 2a \quad \textrm{ .................. (1)} \end{align*}$$

Komponen gaya yang bekerja pada benda 2 :

$$\begin{align*} \Sigma F &= ma \\ F - T &=m_2 a \\ 24 - T &=1a \\ T &= 24 - a \quad \textrm{ .................. (2)} \end{align*}$$

Substitusikan persamaan (1) ke persamaan (2) :

$$\begin{align*} T &= T \\ 2a &=24 - a \\ 3a &=24 \\ a &= 8 \quad \textrm{m/s}^2 \end{align*}$$

Besar tegangan tali :

$$\begin{align*} T &= 2a \\ &=2\cdot 8 \\ &=16\quad \textrm{N} \end{align*}$$

atau :

$$\begin{align*} T &=24 - 8 \\ &=16 \quad \textrm{N} \end{align*}$$

Jawaban : E

Contoh Soal Hukum II Newton Nomor 3

Dua balok bergandengan pada lantai yang licin seperti gambar berikut. 

Sebuah gaya mendatar F = 12 N dikerjakan pada m1. Jika m₁ = 2 kg, m₂ = 4 kg, besar gaya kontak terhadap kedua balok adalah ....

A. 2 N

B. 4 N

C. 8 N

D. 10 N

E. 12 N

Pembahasan :

Kita uraikan gaya - gaya pada masing-masing benda :

Gaya-gaya pada benda m₁ :

$$\begin{align*} \Sigma F&= ma \\ F - F_{21} &=m_1 a \\ 12 - F_{21} &=2 a \\ F_{21} &=12 - 2a \quad \textrm{ ............................ (1)} \end{align*}$$

Gaya – gaya yang bekerja pada benda m₂ :

$$\begin{align*} \Sigma F&= ma \\ F_{12} &=m_2 a \\ F_{12} &=4 a \quad \textrm{ ............................ (2)} \end{align*}$$

Substitusi persamaan (1) ke persamaan (2) :

$$\begin{align*} F_{12} &= F_{21} \\ 4a &=12 - 2a \\ 6a &=12 \\ a & = 2 \quad \textrm{m/s}^2 \end{align*}$$

Besar gaya kontak terhadap kedua balok :

$$\begin{align*} F_{12} &= 4a \\ &=4\cdot 2 \\ &= 8 \quad \textrm{N} \end{align*}$$

Atau :

$$\begin{align*} F_{21} &= 12 - 2a \\ &=12 - 2\cdot 2 \\ &=12 - 4 \\ & = 8 \quad \textrm{N} \end{align*}$$

Jawaban : C

Contoh Soal Hukum II Newton Nomor 4

Benda bermassa 1 kg ditarik oleh gaya mendatar sebesar 2 N dari keadaan diam. Jarak yang ditempuh benda dalam waktu 10 s adalah ....

A. 20 m 

B. 25 m 

C. 100 m 

D. 200 m 

E. 250 m 

Pembahasan :

Percepatan benda :

$$\begin{align*} a &=\frac{F}{m} \\ &=\frac{2}{1} \\  &=2\quad \textrm{m/s}^2 \end{align*}$$

Jarak yang ditempuh benda dalam waktu 10 s :

$$\begin{align*} s &=v_o t + \frac{1}{2}at^2 \\ &=0 \cdot 10 + \frac{1}{2}\cdot 2 \cdot 10^2 \\  &=100\quad \textrm{m} \end{align*}$$

Jawaban : C

Contoh Soal Hukum II Newton Nomor 5

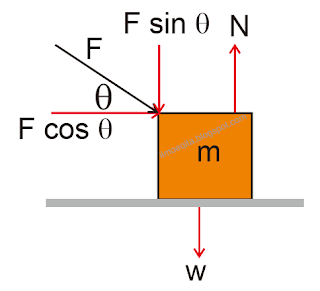
Sebuah balok bermassa m didorong dengan gaya F dengan membentuk sudut θ terhadap arah mendatar seperti gambar berikut. 

Besar gaya normal yang bekerja pada benda adalah ....

A. mg

B. F sin θ – mg

C. F cos θ – mg

D. F sin θ + mg

E. F cos θ + mg

Pembahasan :

$$\begin{align*} \Sigma F_y &= 0\\ N - F \sin \theta - w &=0 \\ N &= F \sin \theta  + w \\ &= F \sin \theta  + mg \end{align*}$$

Jawaban : D

Contoh Soal Hukum II Newton Nomor 6

Sebuah balok bermassa 10 kg mula-mula diam, kemudian bergerak menuruni bidang miring sepanjang 10 m. 

Jika sudut kemiringan 300 dan g = 10 m/s², kelajuan balok saat tiba di dasar bidang miring adalah .....

A. 5 m/s 

B. 7,5 m/s 

C. 10 m/s 

D. 12,5 m/s 

E. 15 m/s 

Pembahasan :

$$\begin{align*} \Sigma F_x &= ma\\ w \sin 30 ^o &=ma \\ 10\cdot 10 \cdot 0,5 &=10 \cdot a \\ a &=5 \quad \textrm{m/s}^2 \end{align*}$$

Kelajuan balok saat tiba di dasar bidang miring :

$$\begin{align*} v_t^2 &= v_o^2 + 2as\\ v_t^2 &=0^2 + 2\cdot 5 \cdot 10 \\ v_t^2 &=100 \\ v_t &=\sqrt{100} \\ &=10 \quad \textrm{m/s} \end{align*}$$

Jawaban : B

Contoh Soal Hukum II Newton Nomor 7

Benda dengan massa 50 kg bergerak dengan kecepatan tetap 4 m/s. Besar gaya perlawanan yang diperlukan agar benda tersebut tepat berhenti 10 m dari tempat semula adalah ....

A. 0,8 N

B. 10 N 

C. 20 N 

D. 40 N 

E. 80 N

Pembahasan :

Perlambatan benda :

$$\begin{align*} v_t^2 &= v_o^2 + 2as\\ 0^2 &=4^2 - 2\cdot a \cdot 10 \\ 20a &= 8 \\ a &=\frac{8}{20} \\ &=0,4 \quad \textrm{m/s}^2 \end{align*}$$

Gaya perlawanan :

$$\begin{align*} F &= ma\\ &=50 \cdot 0,4 \\ &=20 \quad \textrm{N} \end{align*}$$

Jawaban : C

Contoh Soal Hukum II Newton Nomor 8

Dua benda A dan B masing-masing 2 kg dan 3 kg dihubungkan dengan tali melalui katrol seperti gambar berikut (g = 10 m/s²).

Jika lantai dan gesekan antara tali dengan katrol diabaikan, serta benda B bergerak turun, besar tegangan tali T adalah ....

A. 10 N 

B. 12 N 

C. 15 N 

D. 20 N 

E. 28 N 

Pembahasan :

Gaya mendatar yang bekerja pada benda A :

$$\begin{align*} \Sigma F &= ma\\ T &=ma \\ &= 2a \quad \textrm{ ................... (1) } \end{align*}$$

Gaya vertikal yang bekerja pada benda B :

$$\begin{align*} \Sigma F &= ma\\ w - T &=ma \\ mg - T &=ma \\ T &= mg - ma \\ &= 3\cdot 10 - 3a \\ &= 30 - 3a \quad \textrm{ ................... (2) } \end{align*}$$

Substitusikan persamaan (1) ke persamaan (2) :

$$\begin{align*} T &= T\\ 2a &=30 - 3a \\ 5a &=30 \\ a &=6 \quad \textrm{m/s}^2 \end{align*}$$

Menentukan besar tegangan tali menggunakan persamaan 1:

$$\begin{align*} T &=2a \\ &=2\cdot 6 \\ &= 12 \quad \textrm{N} \end{align*}$$

Menentukan besar tegangan tali menggunakan persamaan 2:

$$\begin{align*} T &= 30 - 3a \\ &= 30 - 3\cdot 6 \\ &= 30 - 18 \\ &= 12 \quad \textrm{N} \end{align*}$$

Jawaban : B

Contoh Soal Hukum II Newton Nomor 9

Benda bermassa 1 kg yang terletak di atas tanah ditarik ke atas dengan gaya 15 N selama 2 s, lalu dilepaskan. Tinggi maksimum benda tersebut adalah ....

A. 40 m 

B. 15 m 

C. 10 m 

D. 7,5 m  

E. 5 m

Pembahasan :

Percepatan benda selama 2 sekon : 

$$\begin{align*} \Sigma F &= ma \\F - w&=  ma \\15 - 10&=  1\cdot a \\5&=  1\cdot a \\ a &= 5  \quad \textrm{m/s}^2 \end{align*}$$

Kecepatan benda selama 2 sekon :

$$\begin{align*} v_t &= v_o +at \\v_t &=  0 + 5\cdot2 \\&=  10 \quad \textrm{m/s} \end{align*}$$

Jarak tempuh selama 2 sekon :

$$\begin{align*} s &= v_o t +\frac{1}{2}at^2 \\&=  0\cdot 2 +\frac{1}{2}\cdot 5 \cdot 2^2 \\&=  10 \quad \textrm{m} \end{align*}$$

Tinggi maksimum setelah dilepaskan :

$$\begin{align*} v_t^2 &= v_o^2 -2gh \\0 &=  10^2 -2\cdot 10\cdot h \\20 h &=  100 \\h &=  5 \quad \textrm{m} \end{align*}$$

Total tinggi maksimum benda :

h _maks = s + h = 10 + 5 = 15 m

Jawaban : B

Artikel ini membahas berbagai aspek Hukum Newton, yaitu tiga hukum yang dikemukakan oleh Sir Isaac Newton yang mendasari prinsip-prinsip dasar gerak dan gaya dalam fisika.

Hukum Newton Pertama menyatakan bahwa suatu objek akan tetap dalam keadaan diam atau bergerak lurus beraturan kecuali ada gaya luar yang bekerja padanya. Contoh aplikasi hukum ini adalah ketika mobil yang sedang melaju mendadak berhenti, penumpang di dalamnya akan terdorong ke depan.

Hukum Newton Kedua menjelaskan bahwa percepatan suatu objek berbanding lurus dengan gaya yang bekerja padanya dan berbanding terbalik dengan massanya. Rumus yang digunakan adalah F = m.a dimana F adalah gaya, m adalah massa, dan a adalah percepatan. Contoh aplikasi hukum ini adalah ketika kita mendorong kereta belanja di supermarket; semakin besar gaya yang kita berikan, semakin cepat kereta tersebut bergerak.

Hukum Newton Ketiga menyatakan bahwa setiap aksi selalu menghasilkan reaksi yang sama besar namun berlawanan arah. Contoh dari hukum ini adalah saat kita mendayung perahu, air yang didorong oleh dayung menghasilkan reaksi yang mendorong perahu bergerak maju.

Hukum Newton juga diterapkan dalam berbagai sistem, seperti katrol dan bidang datar. Pemahaman mendalam tentang hukum-hukum ini sangat penting dalam berbagai bidang ilmu pengetahuan dan teknik.

Dengan memahami hukum-hukum Newton, kita dapat lebih baik mengaplikasikan prinsip-prinsip fisika dalam kehidupan sehari-hari dan teknologi.