Jika c adalah kelajuan cahaya di udara, agar massa benda menjadi 125 persennya massa diam, benda harus digerakkan pada kelajuan ....
A. 1,25c
B. 1c
C. 0,8c
D. 0,6c
E. 1,5c
Pembahasan :
m = 1,25mo
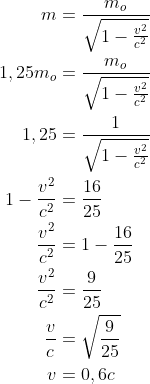
Jawaban : D
Soal UMPTN 1990/Rayon C - Bila kelajuan partikel 0,6c, maka perbandingan massa relativistic partikel itu terhadap massa diamnya adalah ....
A. 5 : 3
B. 25 : 9
C. 5 : 4
D. 25 : 4
E. 8 : 5
Pembahasan :
^2}{c^2}}}&space;\\&space;&=&space;\frac{m_o}{\sqrt{1-0,36}}&space;\\&space;&=&space;\frac{m_o}{\sqrt{0,64}}&space;\end{align*})
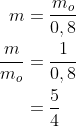
Jawaban : C
A. 1,25c
B. 1c
C. 0,8c
D. 0,6c
E. 1,5c
Pembahasan :
m = 1,25mo
Jawaban : D
Soal dan Pembahasan Relativitas
Soal UMPTN 1990/Rayon C - Bila kelajuan partikel 0,6c, maka perbandingan massa relativistic partikel itu terhadap massa diamnya adalah ....
A. 5 : 3
B. 25 : 9
C. 5 : 4
D. 25 : 4
E. 8 : 5
Pembahasan :
Jawaban : C
