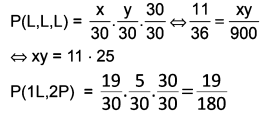Imagine a particle of mass m, constrained to move along the x-axis, subject to some specified force F(x, t). The program of classical mechanics is to deter- mine the position of the particle at any given time: x(t). Once we know that, we can figure out the velocity (\( v=\frac{dx}{dt}\) ), the momentum (p = mv), the kinetic energy ( \( T=\frac{1}{2}mv^2 \) ), or any other dynamical variable of interest. And how do we go about determining x(t)? We apply Newton's second law: F = ma. (For conservative systems the only kind we shall consider, and, fortunately, the only kind that occur at the microscopic level---the force can be expressed as the derivative of a potential energy function, \( F=-\frac{\partial V}{\partial x} \) , and Newton's law reads \( m\frac{d^2x}{dt^2}=-\frac{\partial V}{\partial x} \) .) This, together with appropriate initial conditions (typically the position and velocity at t 0), determines x(t). Quantum mechanics approaches this same problem quite differentl
Soal dan pembahasan peluang - Soal No. 1. Terdapat 5 orang yang akan duduk berderet. Dua di antaranya adalah Rini dan Rina, mereka adalah anak kembar. Apabila mereka tidak ingin duduk bersebelahan, maka peluangnya adalah ....
A. 1/5
B. 2/5
C. 3/5
D. 4/5
E. 1
Pembahasan Soal:
Terdapat 5 orang yang akan duduk berurutan. Untuk mencari peluang agar 2 orang di antaranya tidak duduk bersebelahan dapat lebih mudah jika menggunakan komplemennya.
Komplemennya berarti Rina dan Rini duduk bersebelahan, sehingga Rina dan Rini dianggap satu kesatuan. Sehingga banyaknya cara mereka duduk adalah 4!
Sedangkan Rina dan Rini bebas berpindah di sebelah kanan maupun kiri, sehingga banyaknya posisi duduk Rina dan Rini ada 2!
Sehingga banyaknya cara 5 orang duduk berurutan dengan Rina dan Rini bersebelahan adalah: n(A)=4!2!=4.3.2.1.2.1=48
Sedangkan, semestanya adalah: n(s)=5!=5.4.3.2.1=120
Sehingga, peluang Rina dan Rini bersebelahan adalah :
&space;=&space;\frac{n(A^c)}{n(S)}&space;=&space;\frac{48}{120}&space;=&space;\frac{2}{5} "P(A^c) = \frac{n(A^c)}{n(S)} = \frac{48}{120} = \frac{2}{5}")
Jadi peluang Rina dan Rini tidak bersebelahan pada saat duduk adalah :
&space;=&space;1-&space;P(A^c)=1-\frac{2}{5}&space;=\frac{3}{5} "P(A) = 1- P(A^c)=1-\frac{2}{5} =\frac{3}{5}")
Jawaban : C
Soal No. 2. Sebuah dadu tidak setimbang, dengan peluang muncul angka satu adalah seperempat dari total peluang lainnya. Peluang muncul angka dua dan tiga masing-masing adalah sepertiga dari total peluang lainnya. Apabila dilakukan pelemparan 3 kali, maka peluang muncul angka kurang dari empat sebanyak 2 kali adalah ....
A. 0,576
B. 0,467
C. 0,324
D. 0,216
E. 0,108
Pembahasan Soal :
1) Peluang munculnya angka satu adalah seperempat dari total peluang lainnya :
&space;&=&space;\frac{1}{4}(1-P(1))&space;\\&space;&=&space;\frac{1}{4}-\frac{1}{4}P(1)&space;\\&space;\frac{5}{4}P(1)&=&space;\frac{1}{4}\\&space;P(1)&space;&=&space;\frac{1}{5}&space;\end{align*} "\begin{align*} P(1) &= \frac{1}{4}(1-P(1)) \\ &= \frac{1}{4}-\frac{1}{4}P(1) \\ \frac{5}{4}P(1)&= \frac{1}{4}\\ P(1) &= \frac{1}{5} \end{align*}")
2) Peluang munculnya angka dua dan tiga masing-masing adalah sepertiga dari total peluang lainnya :
==>
3) Peluang munculnya angka kurang dari empat :
4) Dilakukan pelemparan 3 kali, maka peluang muncul angka kurang dari empat sebanyak 2 kali :
Jawaban : B
Soal No. 3. Sebuah dadu bersisi 6 bidang tak beraturan, setiap sisinya diberi nomor 1,2,3,4,5, dan 6. Jika dadu tersebut dilempar, maka akan jatuh pada satu sisi tertentu. Jika P(n) adalah nilai peluang benda tersebut jatuh pada sisi bernomor n dan berlaku
maka nilai x adalah ....
Banyaknya bilangan ratusan dengan angka pertama dan kedua mempunyai selisih 2 :
Banyaknya bilangan seluruhnya adalah : 10 + 20 + 20 + 20 + 20 + 20 + 20 + 10 + 10 = 150 bilangan
Jawaban : D
Soal No. 5 . Di dalam kotak terdapat 12 bola putih dan 3 bola merah. Di dalam kotak II terdapat 4 bola putih dan 4 bola merah. Jika dari kotak I dan II masing-masing diambil 2 bola satu per satu dengan pengambilan, maka peluang yang terambil adalah 1 bola merah adalah ....
A. 0,04
B. 0,10
C. 0,16
D. 0,32
E. 0,40
Pembahasan :
Dari kotak I dan II masing-masing diambil 2 bola satu per satu dengan pengambilan, kejadian dengan pengambilan 1 bola merah adalah
Soal No. 7. Dari 15 anak yang terdiri dari laki-laki dan perempuan akan diambil dua anak bersamaan. Jika banyak kemungkinan terambil laki-laki dan perempaun adalah 26, maka jumlah selisih laki-laki dan perempuan adalah ....
A. 13
B. 11
C. 9
D. 5
E. 3
Pembahasan :
Dari 15 anak, diambil 2 anak bersamaan.
Banyaknya kemungkinan terambil laki-laki dan perempuan adalah 26.
Misal banyaknya anak laki-laki adalah l , maka banyaknya anak perempuan adalah 15-l
Bila l = 2, maka P = 15 -2 = 13, sehingga 13 -2 = 11
Bila l = 13 , maka P = 15 - 13 = 2, sehingga 13 - 2 = 11
Jawaban : B
A. 1/5
B. 2/5
C. 3/5
D. 4/5
E. 1
Pembahasan Soal:
Terdapat 5 orang yang akan duduk berurutan. Untuk mencari peluang agar 2 orang di antaranya tidak duduk bersebelahan dapat lebih mudah jika menggunakan komplemennya.
Komplemennya berarti Rina dan Rini duduk bersebelahan, sehingga Rina dan Rini dianggap satu kesatuan. Sehingga banyaknya cara mereka duduk adalah 4!
Sedangkan Rina dan Rini bebas berpindah di sebelah kanan maupun kiri, sehingga banyaknya posisi duduk Rina dan Rini ada 2!
Sehingga banyaknya cara 5 orang duduk berurutan dengan Rina dan Rini bersebelahan adalah: n(A)=4!2!=4.3.2.1.2.1=48
Sedangkan, semestanya adalah: n(s)=5!=5.4.3.2.1=120
Sehingga, peluang Rina dan Rini bersebelahan adalah :
Jadi peluang Rina dan Rini tidak bersebelahan pada saat duduk adalah :
Jawaban : C
Soal No. 2. Sebuah dadu tidak setimbang, dengan peluang muncul angka satu adalah seperempat dari total peluang lainnya. Peluang muncul angka dua dan tiga masing-masing adalah sepertiga dari total peluang lainnya. Apabila dilakukan pelemparan 3 kali, maka peluang muncul angka kurang dari empat sebanyak 2 kali adalah ....
A. 0,576
B. 0,467
C. 0,324
D. 0,216
E. 0,108
Pembahasan Soal :
1) Peluang munculnya angka satu adalah seperempat dari total peluang lainnya :
2) Peluang munculnya angka dua dan tiga masing-masing adalah sepertiga dari total peluang lainnya :
Soal No. 3. Sebuah dadu bersisi 6 bidang tak beraturan, setiap sisinya diberi nomor 1,2,3,4,5, dan 6. Jika dadu tersebut dilempar, maka akan jatuh pada satu sisi tertentu. Jika P(n) adalah nilai peluang benda tersebut jatuh pada sisi bernomor n dan berlaku
Pembahasan :
Diketahui :
P(n) adalah peluang munculnya sisi mata dadu bernomor n.
Karena ada enam nomor maka berlaku :
Jawaban : D
Soal No. 4. Banyaknya bilangan ratusan dengan angka pertama dan kedua mempunyai selisih 2 adalah ....
A. 120
B. 130
C. 140
D. 150
E. 160
Pembahasan :
Banyaknya bilangan ratusan dengan angka pertama dan kedua mempunyai selisih 2 :
- Jika angka pertama 1 (1 pilihan), maka angka keduanya 3 (1 pilihan) dan angka ketiga ada 10 pilihan (karena tidak ada aturan boleh berulang atau tidak). Banyaknya ada = 1x1x10 = 10
- Angka pertama 2, angka kedua 0 atau 4, maka banyaknya = 1x2x10 = 20
- Angka pertama 3, angka kedua 1 atau 5, maka banyaknya = 1x2x10 = 20
- Angka pertama 4, angka kedua 2 atau 6, maka banyaknya = 1x2x10 = 20
- Angka pertama 5, angka kedua 3 atau 7, maka banyaknya = 1x2x10 = 20
- Angka pertama 6, angka kedua 4 atau 8, maka banyaknya = 1x2x10 = 20
- Angka pertama 7, angka kedua 5 atau 9, maka banyaknya = 1x2x10 = 20
- Angka pertama 8, angka kedua 6, maka banyak-nya = 1x1x10 = 10
- Angka pertama 9, maka angka kedua 7, maka banyaknya = 1x1x10 = 10
Banyaknya bilangan seluruhnya adalah : 10 + 20 + 20 + 20 + 20 + 20 + 20 + 10 + 10 = 150 bilangan
Jawaban : D
Soal No. 5 . Di dalam kotak terdapat 12 bola putih dan 3 bola merah. Di dalam kotak II terdapat 4 bola putih dan 4 bola merah. Jika dari kotak I dan II masing-masing diambil 2 bola satu per satu dengan pengambilan, maka peluang yang terambil adalah 1 bola merah adalah ....
A. 0,04
B. 0,10
C. 0,16
D. 0,32
E. 0,40
Pembahasan :
Maka, peluang pengambilan satu bola merah adalah :
Jawaban : E
Soal No. 6. Tiga kelas masing-masing terdiri atas 30 mahasiswa. Satu kelas di antaranya terdiri atas siswa laki-laki saja. Satu siswa dipilih dari tiap-tiap kelas. Peluang terpilih ketiganya lahi-laki adalah 11/36 . Peluang terpilihnya paling paling sedikit seorang di antaranya laki-laki adalah ....
Pembahasan :
Berdasarkan keterangan pada soal, diperoleh :
Sehingga diperoleh :
Jadi peluang terpilih paling sedikit seorang di antaranya laki-laki adalah 19/180
Jawaban : B
Soal No. 7. Dari 15 anak yang terdiri dari laki-laki dan perempuan akan diambil dua anak bersamaan. Jika banyak kemungkinan terambil laki-laki dan perempaun adalah 26, maka jumlah selisih laki-laki dan perempuan adalah ....
A. 13
B. 11
C. 9
D. 5
E. 3
Pembahasan :
Dari 15 anak, diambil 2 anak bersamaan.
Banyaknya kemungkinan terambil laki-laki dan perempuan adalah 26.
Misal banyaknya anak laki-laki adalah l , maka banyaknya anak perempuan adalah 15-l
Bila l = 13 , maka P = 15 - 13 = 2, sehingga 13 - 2 = 11
Jawaban : B
Comments
Post a Comment