Imagine a particle of mass m, constrained to move along the x-axis, subject to some specified force F(x, t). The program of classical mechanics is to deter- mine the position of the particle at any given time: x(t). Once we know that, we can figure out the velocity (\( v=\frac{dx}{dt}\) ), the momentum (p = mv), the kinetic energy ( \( T=\frac{1}{2}mv^2 \) ), or any other dynamical variable of interest. And how do we go about determining x(t)? We apply Newton's second law: F = ma. (For conservative systems the only kind we shall consider, and, fortunately, the only kind that occur at the microscopic level---the force can be expressed as the derivative of a potential energy function, \( F=-\frac{\partial V}{\partial x} \) , and Newton's law reads \( m\frac{d^2x}{dt^2}=-\frac{\partial V}{\partial x} \) .) This, together with appropriate initial conditions (typically the position and velocity at t 0), determines x(t). Quantum mechanics approaches this same problem quite differentl...
Gaya Gerak Listrik Induksi (GGL Induksi)
Jika kutub utara magnet batang digerakkan mendekati atau menjauhi kumparan berarti jumlah garis gaya magnetik yang melingkari kumparan berubah-ubah dan ternyata jarum galvanometer menyimpang, sedangkan jika magnetik batang tidak digerakkan berarti jumlah garis gaya magnetik yang melingkupi kumparan tetap dan ternyata jarum galvanometer tidak menyimpang. Berdasarkan percobaan tersebut, Faraday menyimpulkan bahwa perubahan garis gaya magnetik yang melingkupi kumparan dapat menimbulkan beda potensial pada ujung-ujung kumparan yang disebut arus induksi. Besar arus induksi yang tidak tetap dan arahnya berubah-ubah yang disebut arus bolak-balik.
Hukum-hukum Induksi Elektromagnetik
a. Hukum Faraday
Besarnya GGL induksi yang terjadi pada suatu penghantar bergantung pada cepat perubahan garis gaya magnetik dalam kumparan dan banyaknya lilitan kumparan.
Untuk membuktikan hukum Faraday digunakan batang AB yang digerakkan dalam medan magnetik menjauhi pengamat.
dengan :
N = jumlah lilitan
= perubahan fluks magnetik (Wb)
A = luas bidang yang ditembus (m2)
B = induksi magnet ( T atau Wb/m2)
= selang waktu (s)
l = panjang kawat AB (m)
v = kecepatan gerak batang AB ( m/s )
= ggl induksi (V)
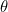= sudut antara v terhadap arah B atau antara B dengan A
Kuat arus yang mengalir dalam batang AB adalah sebagai berikut :
Gaya Lorentz yang bekerja pada batang AB adalah sebagai berikut :
dengan :
R = resistor (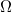
)
I = kuat arus (A)
F = gaya Lorentz ( N)
Jika batang AB diletakkan horisontal, besar gaya Lorentznya adalah sebagai berikut.
dengan
F = gaya Lorentz ( N )
w = mg = berat batang AB
vT = kecepatan terminal (m/s)
b. Hukum Lenz
Arah arus Induksi dalam suatu penghantar itu sedemikian rupa sehingga menimbulkan medan magnet yang melawan perubahan garis gaya magnetik yang menimbulkannya (arah gerak batang selalu berlawanan dengan gaya Lorentz) yang dinyatakan dengan persamaan berikut.
Jika kutub utara magnet batang digerakkan mendekati atau menjauhi kumparan berarti jumlah garis gaya magnetik yang melingkari kumparan berubah-ubah dan ternyata jarum galvanometer menyimpang, sedangkan jika magnetik batang tidak digerakkan berarti jumlah garis gaya magnetik yang melingkupi kumparan tetap dan ternyata jarum galvanometer tidak menyimpang. Berdasarkan percobaan tersebut, Faraday menyimpulkan bahwa perubahan garis gaya magnetik yang melingkupi kumparan dapat menimbulkan beda potensial pada ujung-ujung kumparan yang disebut arus induksi. Besar arus induksi yang tidak tetap dan arahnya berubah-ubah yang disebut arus bolak-balik.
Hukum-hukum Induksi Elektromagnetik
a. Hukum Faraday
Besarnya GGL induksi yang terjadi pada suatu penghantar bergantung pada cepat perubahan garis gaya magnetik dalam kumparan dan banyaknya lilitan kumparan.
Untuk membuktikan hukum Faraday digunakan batang AB yang digerakkan dalam medan magnetik menjauhi pengamat.
N = jumlah lilitan
A = luas bidang yang ditembus (m2)
B = induksi magnet ( T atau Wb/m2)
l = panjang kawat AB (m)
v = kecepatan gerak batang AB ( m/s )
Kuat arus yang mengalir dalam batang AB adalah sebagai berikut :
Gaya Lorentz yang bekerja pada batang AB adalah sebagai berikut :
dengan :
R = resistor (
I = kuat arus (A)
F = gaya Lorentz ( N)
Jika batang AB diletakkan horisontal, besar gaya Lorentznya adalah sebagai berikut.
F = gaya Lorentz ( N )
w = mg = berat batang AB
vT = kecepatan terminal (m/s)
b. Hukum Lenz
Arah arus Induksi dalam suatu penghantar itu sedemikian rupa sehingga menimbulkan medan magnet yang melawan perubahan garis gaya magnetik yang menimbulkannya (arah gerak batang selalu berlawanan dengan gaya Lorentz) yang dinyatakan dengan persamaan berikut.
This comment has been removed by a blog administrator.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDelete